六、高级排序---快速排序

算法
算法
发布日期:   2020-11-01

一、排序原理

1.首先设定一个分界值，通过该分界值将数组分成左右两部分；

2.将大于或等于分界值的数据放到到数组右边，小于分界值的数据放到数组的左边。此时左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值；

3.然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。

4.重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后，整个数组的排序也就完成了。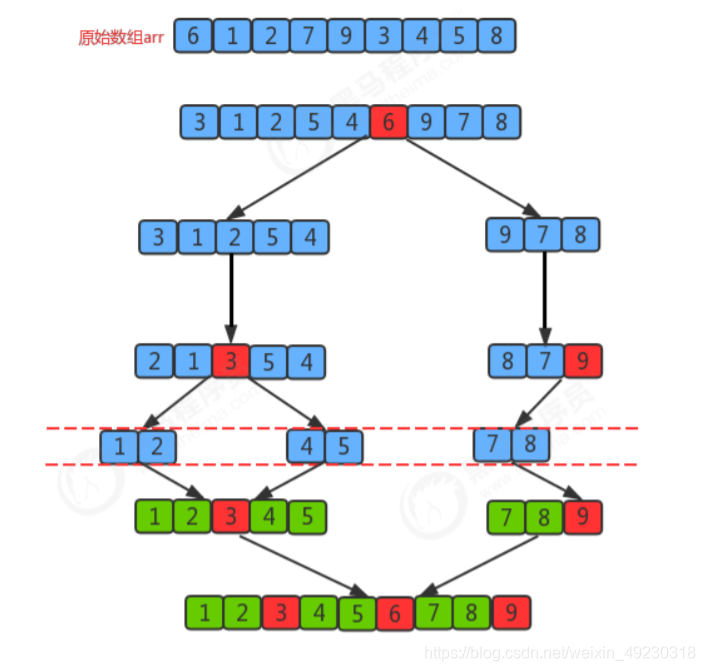
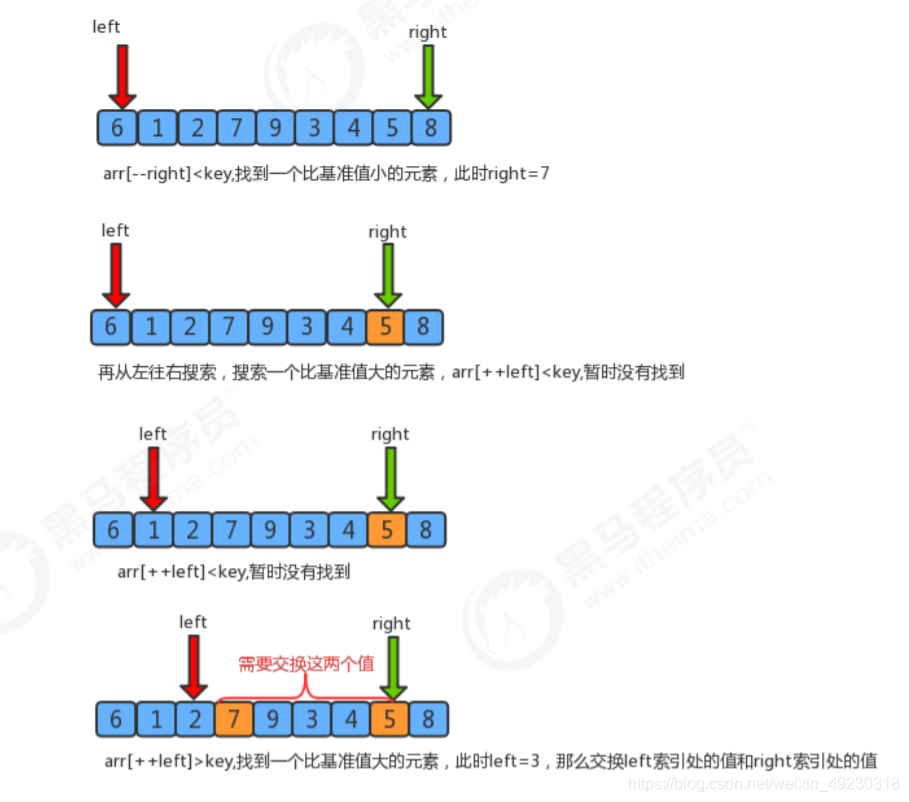
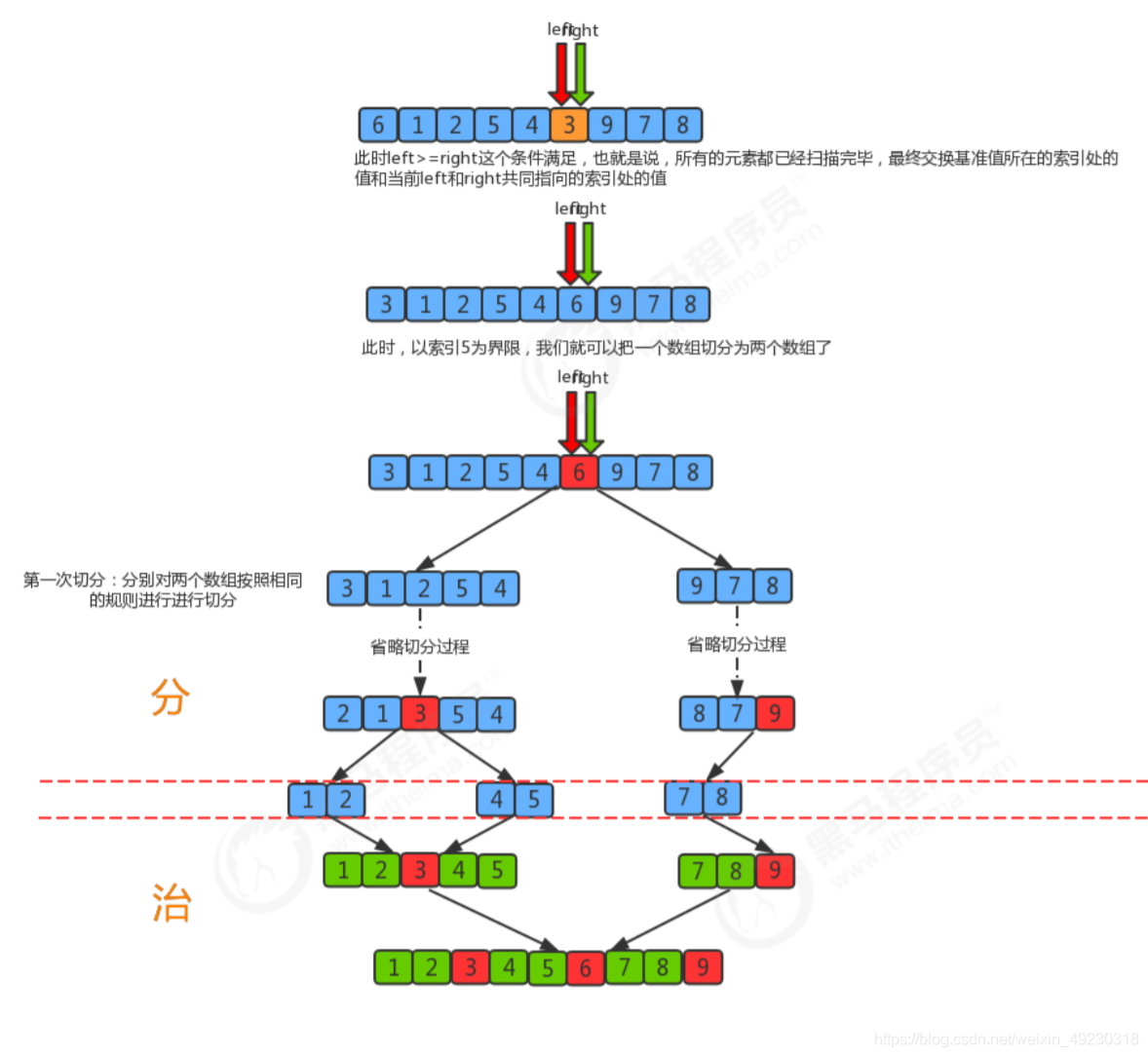
在这里插入图片描述

二、切分原理

把一个数组切分成两个子数组的基本思想：

  1. 找一个基准值（默认第一个元素），用两个指针分别指向数组的头部和尾部；

  2. 先从尾部向头部开始搜索一个比基准值小的元素，搜索到即停止，并记录指针的位置；

  3. 再从头部向尾部开始搜索一个比基准值大的元素，搜索到即停止，并记录指针的位置；

  4. 交换当前左边指针位置和右边指针位置的元素；

  5. 重复2,3,4步骤，直到左边指针的值大于右边指针的值停止。
    在这里插入图片描述
    在这里插入图片描述

    三、代码实现

    public class Quick {
 /*
   比较v元素是否小于w元素
*/
 private static boolean less(Comparable v, Comparable w) {

     return v.compareTo(w) < 0;
 }



/*

数组元素i和j交换位置
*/
private static void exch(Comparable[] a, int i, int j) {
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}

//对数组内的元素进行排序
public static void sort(Comparable[] a) {
    int lo = 0;
    int hi = a.length-1;
    sort(a,lo,hi);
}

//对数组a中从索引lo到索引hi之间的元素进行排序
private static void sort(Comparable[] a, int lo, int hi) {
    //安全性校验
    if (hi<=lo){
        return;
    }

    //需要对数组中lo索引到hi索引处的元素进行分组（左子组和右子组）；
    int partition = partition(a, lo, hi);//返回的是分组的分界值所在的索引，分界值位置变换后的索引

    //让左子组有序
    sort(a,lo,partition-1);

    //让右子组有序
    sort(a,partition+1,hi);
}

//对数组a中，从索引 lo到索引 hi之间的元素进行分组，并返回分组界限对应的索引
public static int partition(Comparable[] a, int lo, int hi) {
   //确定分界值
    Comparable key = a[lo];
    //定义两个指针，分别指向待切分元素的最小索引处和最大索引处的下一个位置
    int left=lo;
    int right=hi+1;

    //切分
    while(true){
        //先从右往左扫描，移动right指针，找到一个比分界值小的元素，停止
        while(less(key,a[--right])){
            if (right==lo){
                break;
            }
        }

        //再从左往右扫描，移动left指针，找到一个比分界值大的元素，停止
        while(less(a[++left],key)){
            if (left==hi){
                break;
            }
        }
        //判断 left>=right,如果是，则证明元素扫描完毕，结束循环，如果不是，则交换元素即可
        if (left>=right){
            break;
        }else{
            exch(a,left,right);
        }
    }

    //交换分界值
    exch(a,lo,right);
    System.out.println(Arrays.toString(a));
    return right;
}

public static void main(String[] args) {
    Integer[] a = {3,4,8,3,8,7,2,5,2,7};
}

}

# 四、时间复杂度分析
**快速排序和归并排序的区别：**
快速排序是另外一种分治的排序算法，它将一个数组分成两个子数组，将两部分独立的排序。

快速排序和归并排序是互补的：归并排序将数组分成两个子数组分别排序，并将有序的子数组归并从而将整个数组排序，而快速排序的方式则是当两个数组都有序时，整个数组自然就有序了。

在归并排序中，一个数组被等分为两半，归并调用发生在处理整个数组之前，在快速排序中，切分数组的位置取决于数组的内容，递归调用发生在处理整个数组之后。

**快速排序时间复杂度分析：**
快速排序的一次切分从两头开始交替搜索，直到left和right重合，因此，一次切分算法的时间复杂度为O(n),但整个快速排序的时间复杂度和切分的次数相关。

**最优情况**：每一次切分选择的基准数字刚好将当前序列等分。
最优情况下快速排序的时间复杂度为O(nlogn);

**最坏情况**：每一次切分选择的基准数字是当前序列中最大数或者最小数，这使得每次切分都会有一个子组，那么总
共就得切分n次，所以，最坏情况下，快速排序的时间复杂度为O(n^2);

**平均情况**：每一次切分选择的基准数字不是最大值和最小值，也不是中值，这种情况我们也可以用数学归纳法证明，快速排序的时间复杂度为O(nlogn)
算法
  目录